GEOMETRÍA DESCRIPTIVA

La geometría descriptiva se define como la rama de las matemáticas que analiza los cuerpos en el espacio representando los objetos de tres dimensiones con representaciones bidimensionales.

 Un objeto puede representarse mediante un isométrico donde se combinan todas las perspectivas o colocando cada una de las vistas mediante proyecciones (FRONTALES, LATERALES, SUPERIORES).

Para representar un punto en forma bidimencional en un plano se realiza una rotación de los planos en sentido horario de tal manera que los planos se empalmen en forma vertical, como muestra el siguiente diagrama.

La distancia horizontal recibe el nombre de ALEJAMIENTO y la vertical de COTA.

  

CONCEPTOS DE  PROYECCIÓN 

O. Identificar el concepto de proyección.

Una proyección es la representación de un objeto tridimensional en una representación bidimensional.

 Los elementos de una proyección son:

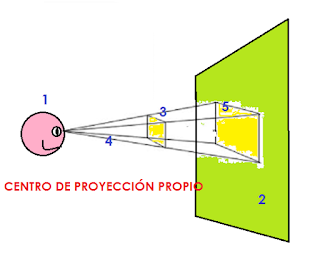
1) OBSERVADOR: Se conoce como centro de proyección y es el punto donde concurren los rayos de proyección y puede estar ubicado en cualquier parte del espacio, si tiene una distancia finita se conoce como centro de proyección propio, si se tiene una distancia infinita (los rayos de proyección son paralelos) se le denomina como proyección impropia.

2)PLANO DE PROYECCIÓN:Es un plano colocado a una distancia arbitraria donde se representa la proyección del objeto.

3)OBJETO: Es el elemento a representar.

4) RAYOS PROYECTANTES:  Son las rectas que unen el centro de proyección con los puntos del objeto y se proyectan en el plano. 

5) PROYECCIÓN: Es la representación en el plano del objeto en forma bidimensional.

TIPOS DE PROYECCIÓN.

De acuerdo a la posición del observador se pueden clasificar las proyecciones como se representa en el siguiente esquema.

A) PROYECCIÓN CÓNICA ORTOGONAL: es aquella proyección donde las líneas de proyección concurren en un punto central y estos se presentan en forma horizontal.

B) PROYECCIÓN CÓNICA OBLICUA: es aquella proyección en donde el observador y el plano de proyección se encuentra a diferente altura como muestra el siguiente esquema.

C)PROYECCIÓN PARALELA ORTOGONAL: es aquella en donde el observador se encuentra a una distancia indefinida del plano de proyección, por tanto las líneas de proyección son paralelas.

D) PROYECCIÓN PARALELA OBLICUA: en esta proyección, las líneas de proyección se representan en forma diagonal como muestra el siguiente esquema.

Una proyección permite representar un isométrico (representación de un objeto sin alterar sus proporciones) utilizando diferentes transformaciones entre los cuales se encuentran:

A)TRASLACIÓN: es el cambio de ubicación de los puntos de una figura plana en una misma dirección, sentido y longitud, s puede representar el movimiento mediante flechas que recibe el nombre de vectores.

B)REFLEXIÓN: es una representación de una figura original a otra llamada eje de simetría utilizando rectas perpendiculares como muestra el siguiente esquema.

C) SIMETRÍA CENTRAL: en esta transformación se realiza la imagen utilizando proyecciones de los puntos de la figura que convergen en u punto llamado punto de simetría trasladando las distancias con el compás. 

 D) ROTACIÓN: esta transformación se realiza a partir de un punto de rotación determinado, se realiza en forma positiva en sentido anti-horario y en negativa en sentido horario.

Ejercicio:

Realice un triángulo de 3,6,6 y realice la traslación a 9 cm.

Pasos:

1.- Marque la base de 3 cm.

2.- Abra el compás a 6 cm.

3.-Coloque el compás en el puno A, y trace una linea.

4.- Coloque el compás en el puno B, y trace una línea.

5.- Forme el triángulo.

6.- Con la regla trace una linea desde el punto A de 9 cm.

7.-Con la regla trace una linea desde el punto B de 9 cm.

8.-Con la regla trace una linea desde el punto C de 9 cm.

9.- Finalmente trace su triangulo que se forma con las lineas anteriores.

ISOMÉTRICO.

O. Representar un objeto en un sistema tridimensional.

Un isométrico representa un objeto en forma tridimensional utilizando proyecciones con una inclinación de 30° con respecto a la horizontal para conservar las medidas ya sea a escala o con su valor real.

Ejercicio:

Realice un cubo de 4 cm de aristas en un simétrico.

1.- Marque una linea de 8 cm, posteriormente marque una linea de 6 cm sobre la misma.

2.- Con el transportador marque de lado derecho e izquierdo un angulo de 30°, marque las lineas.

3.- Marque la base de 4 cm de lado derecho.

4.- Marque la profundidad de lado izquierdo de 4 cm.

5.- Marque la altura de 4 cm en el centro. 

6.-Colo que las escuadra de 45° y de 30° de manera que la escuadra de 30° quede alineada con la linea marcada del lado izquierdo para trazar las aristas,

ISOMETRICAS.

O.representar un objeto en isometricas.

La escala se define como una representación de un objeto en forma proporcional donde  se puede calcular la proporción mediante la siguiente ecuación:

ESCALA=DIBUJO/REALIDAD

Cuando se realiza una representación donde se incremente los valores de cada magnitud la relación debe ser mayor a 1, en caso contrario la relación es menor a 1.

Para representar una escala es lugar de diagonal se representa con 2:  como muestra la siguiente proporción.

2:1  5:1  100:25 AMPLIACIÓN

1:2     3:1   100:125 REDUCCION

Ejercicio:

Realice el isométrico de un prisma utilizando la escala 2:1.

1.-Trace una linea de  8 cm.un centímetro menos de la linea trace otra vertical.

2.- Marque los ángulos de 30°.

3.-Marque la base  de  6 cm.

4.-Marque la profundidad  de  6 cm.

5.-Marque la altura de  4 cm.

6.- Para trazar las demás aristas coloque las escuadra de manera que queden ala misma posición que la linea de profundidad.

SISTEMA DE COORDENADAS.

O. Representar un punto en el espacio, calculas la medidas de las aristas de un objeto.

Un sistema de 3 dimensiones cuentas con 3 ejes  perpendiculares entre sí, los cuales permiten ubicar un punto en el espacio mediante proyecciones en cada uno de los ejes los cuales forman octantes que son proyecciones en planos formados por los ejes.

Los octantes  se colocan en sentido anti.horario indicando en la vista frontal del observador.

Para ubicar un punto en el espacio se utiliza por convención los ejes X,Y,Z  en la siguiente posición

Para representar un punto se hacen proyecciones como se indica:

a= pto. (3,4,2)

b= pto. (3,0,1)

c= pto (-2,4,0)

Para calcular la distancia entre dos puntos se utiliza teorema de pitágoras  utilizando el incremento en cada uno de los ejes.

.

PUNTO DE ESPACIO TRIDIMENSIONAL.

O. Identificar las coordenadas y las aristas de un objeto.

para identificar las vértices y aristas de un objeto es importante identificar el punto de referencia sonde será colocado el sistema de coordenadas de cada una de las vertices.

Las coordenadas permiten encontrar las mendidas de dos aristas considerando la distancia entre los puntos.

 Pasos para resolver:

1.- trazas los ejes x,y,z.

2.-Tazas tu figura de acuerdo al eje donde se ubique.

3.- A cada arista colocales una letra del abecedario para que sea mas fácil identificarlos.

4.- Toma de referencia los cuadritos para ubicar la posición de la arista.

5.- Por ejemplo si ubicamos la arista A sus coordenadas serían (0,0,0) porque no se mueve para ninguno delos ejes X y Z.

VISTAS DE UN OBJETO.

O. Identificar la proyección de las caras de un objeto.

Un objeto (Prisma) cuenta principalmente con 6 caras que pueden representarse mediante proyecciones  como muestra el siguiente esquema.

Ejercicio:

Pasos:

1.- Realiza tu prisma.

2.- Traza todas las lineas imaginarias de 30° tomando como referencia todas las aristas de tu prisma.

3.- Una vez trazado las lineas imaginarias, abre tu combas a 5 cm.

4.- Colocado el cada una de las aristas y marca con una pequeña linea.

5.- Repite los mismos pasos en cada cara de tu prima.

  ÁNGULOS.

O. Identificar la magnitud de un angulo con ecuaciones.

Un angulo se define como la abertura entre dos rectas , seguido d elos puntos que conforman al segmento a su vértice.

En el sistema internacional se utiliza los degradientes que dividen a una circunferencia en 360°.

El sistema absoluto utiliza radianes que son la división de una circunferencia de 2π radianes.

Para calcular el valor de 1 o varios ángulos a partir de un esquema se debe encontrar la ecuación como muestra el siguiente ejemplo:

PASOS:

1.-Formula la ecuación empezando por la letra A.

2.- Una vez realizado la ecuación, se suman toas las x, después se hace la operación de los números sin x.

3.- Una vez obtenido el resultado de la ecuación se multiplica cada numero por el resultado de la ecuación anterior.

4..- al terminar las multiplicaciones se sumara los resultados que se obtuvieron, y al final de la suma ese será tu resultado.