T.ELIPSE

Una Elipse se define como una cónica formada cuando se realiza un corte en diagonal a un cono en forma análoga a la parábola, es una cónica formada por dos parábolas que cuentan con el mismo eje simétrico y su concavidad es opuesta.

Sus elementos importantes son:

     a)Vértice                                                 e) Eje Menor(Ancho de la parábola)

     b)Foco                                                      f)  Directriz

c  c)Lado Recto                                           g) Excentricidad

     d)Eje Mayor(distancia entre vértices) 

Para Calcular los Elementos de una parábola cuando el centro se encuentra en el origen se deben identificar los valores de la distancia focal, la distancia del foco al centro y la distancia al eje menor (A, B, C).

Las Ecuaciones matemáticas utilizadas en esta cónica se representan en el siguiente esquema:

c=√a²-b²                                

  LR=2 b² /a      

b=√a²-c²

Eje Mayor= 2a

Eje Menor=2b

Excentricidad=c/a

x² + y²  =

a²      b²

a= distancia centro-vértice

b= distancia centro-Eje Menor

c= distancia centro-Foco

 T. ELIPSE

Una elipse es un lugar geométrico que se forma a partir de un corte diagonal o un cono.

Su ecuación se define como una ecuación cuadrática donde la variable dependiente e independiente son de segundo grado, de diferente coeficiente y de signo positivo.

Las siguientes ecuaciones representan en forma gráfica lugares geométricos.

x²+y²=4

X	Y
-3	Ind
-2	0
-1	1.7320
0	2
1	1.7320
2	0
3	Ind

 

 

T. ELIPSE

O. Resolver ejercicios de aplicación de la elipse.

Ejemplo:

Un terreno tiene un frente de 50m de este a oeste y una profundidad de 30m de norte a sur, si se desea sembrar arboles en forma elíptica que toque a la mitad en cada uno de los lados y se desea colocar dos caminos en forma análoga  a los lados rectos, indique la magnitud total de los caminos y la ecuación general de los árboles.

T. HIPÉRBOLA

O. Identificar los elementos de la hipérbola.

La hipérbola es una cónica formada por un corte vertical a dos conos concéntricos encontrados entre sí, donde se representa mediante una ecuación de segundo grado donde las variables cuadráticas son de signos diferentes.

Para identificar sus elementos es indispensable identificar las variables:

                                                                                                                                                                a = distancia entre centro - vértice.

b = distancia entre centro - eje transverso.

c = distancia entre centro - foco.

La excentricidad es mayor o igual a 1 y sus elementos se calculan de las siguientes expresiones:

Hipérbola.

O. identificar los elementos de la hipérbola con centro fuera del origen.

Cuando una hipérbola no se encuentra en el origen sus elementos se representan en función del centro como muestra los siguientes esquemas:

Ejemplo:

una hipérbola tiene centro en el punto (2,4), vértice en el punto (2,8) y foco en el punto (2, -1).

Indique sus elemento de manera gráfica y representa su ecuación general.

T. SISTEMA POLAR.

O. Realizar conversiones entre coordenadas polares y rectangulares.

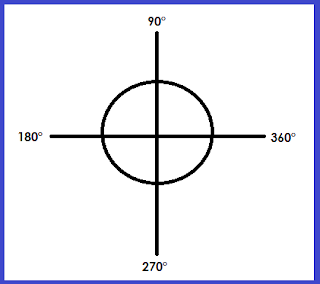
Un sistema rectangular se compone por ejes perpendiculares que cuentan con proyecciones para ubicar un punto en el plano, un sistema polar cuenta con círculos concéntricos que representa la magnitud y radios homogéneos que representan el ángulo de inclinación.

Para calcular un punto en coordenadas polares se utiliza la siguiente ecuación:

Para convertir una coordenada rectangular en polar se utiliza las siguientes ecuaciones:

T. ECUACIONES EN SISTEMAS POLARES.

O. Graficar caracoles, rosas, lemins catas y espirales en sistema polar.

Para graficar una ecuación se debe tener una variable independiente, en el sistema polar la variable dependiente es generalmente el ángulo, los principales lugares  geométricos (casos especiales) son: caracoles , rosas, lemins catas y espirales.

Ejemplo: 

Grafique e indique el nombre de la siguiente ecuación:

ÁREA DE POLÍGONOS.

O. Calcula el área del polígono conociendo sus vértices.

Para calcular el área de un polígono conociendo sus vértices se realiza una determinante con cada uno de ellos matemáticamente se puede expresar con la siguiente ecuación.

Ejemplo:

Indique el área del polígono formado por los puntos:

A (-3,-4)

B (1,-3)

C (4,6)

D (3,7)

E(-3, 1)

Pasos:
-Ubica los puntos en la gráfica.
-Multiplica los números en diagonal empezando de la derecha.
-Multiplica los números desde abajo empezando de izquierda.
-Los resultados se colocan en los corchetes dentro de los paréntesis.
-Restas ambos resultados.
-Los divides entre 1/2.

RECTA.

O. identificar la ecuación de la recta "General", pendiente, ordenada al origen y dos puntos.

La recta de defina como un conjunto de puntos uni-direccionados que cuentan con una pendiente (relación entre coordenadas y abscisas) y un ángulo de inclinación, matemáticamente se calcula la siguiente  ecuación.

La recta se puede representar de diversas formas

a)Pendiente ordenada al origen.

b) Fórmula general.

c) Forma dos puntos.

d) Forma punto Pendiente.

e) Forma reducida..

A) PENDIENTE ORDENADA AL ORIGEN.

Como su nombre lo dice se debe conocer el valor de la pendiente y el punto donde este corta al eje de las ordenadas, se representa despejando a la ordenada de la ecuación es recomendable utilizar esta ecuación  

Ejemplo:

Indique la ecuación pendiente ordenada de origen que pasa por lo puntos (-1,-4) y (2,0).

-Ubica las coordenadas en la gráfica y trázala.
-Resuelve la ecuación m=Y2-Y1/X2-X1.
-Resuelve la ecuación de centígrados. 
-Una vez obtenido el resultado, acomoda la ecuación ordenada al origen.

B) FORMA GENERAL.

Cuando se tiene dos puntos  es recomendable utilizar este ecuación antes de indicar, las ecuaciones restantes, la ecuación general se representa cuando la ecuación se iguala a 0.  

Ejemplo:   

Grafique y represente en forma general las siguientes ecuaciones.

-En la ecuación ubica m y b.

- En la ecuación de angulo de inclinación sustituye a m.

-Sustituye la formula general.

- El punto b sale de donde cruza la recta.

C) ECUACIÓN DOS PUNTOS.

D) PUNTO PENDIENTE.

O. Representar a la recta en su forma reducida y punto pendiente.

Para representar una recta conociendo un punto por donde pasa y la pendiente o ángulo de inclinación se utiliza la ecuación:

A partir de esta ecuación se puede encontrar las ecuaciones restantes, como indica los siguientes ejemplos:

-Para resolver este tipo de gráfica, se tiene que llevar a caco la resolución de la primera ecuación.

-Cada ecuación que vallas realizando solo hay que sustituirla.

-Una vez terminado realizas la grafica. 

RESOLVER PROBLEMAS DE APLICACIÓN.

Para resolver un problema de aplicación se debe diseñar un esquema que muestre gráficamente, las variables del problema.
Ejemplo:

Un edidfico de 40m de altura une sus puntos mas altos con otro edificio con 32m de altura que se encuentran separados a una distancia de 50 m indique la ecuación Pendiente O.O que describe la unión de los edificios. Indique la altura de la recta a 10m del edificio más alto.

 -Primero se identifican los datos que plantearon en el problemas.

-Una vez echo el primer paso, se ubica la ecuación que se realizara primero.

- Los datos del problemas se sustituyen en la ecuación, posteriormente se va realizando.

D) FORMA REDUCIDA.

O. Representar una recta en todas sus formas.

El valor de a y b indica el punto donde la recta corta a los ejes coordenados gráficamente. 

Pasos:

-Para resolver este tema, primero se tiene que identificar la ecuación.

-cuando llegue a la ecuación reducida se sustituye la letra a por el 0.

-Una vez realizados esto coloca en la grafican donde se ubica el puntos a.

CIRCUNFERENCIA.

O. identificar la ecuación de la circunferencia con centro en el origen.

Las cónicas se definen  como aquellos lugares geométricos que se forman a partir de cortes realizados o un cono, si el cono se corta en forma horizontal se obtiene una circunferencia, si el corte se realiza en forma diagonal se obtiene una elipse, si el corte se realiza vertical se obtiene una parábola, si el corte se realiza a dos conos con-céntricos se obtiene una hipérbola. 

Una circunferencia se define como el lugar geométrico formado por puntos equidistantes a un punto llamado centro  y cualquier punto se denomina rápido.Cuando una circunferencia tiene su centro en el origen ser representa matemáticamente con la siguiente ecuación.

 Circunferencia.

O. Identificar la ecuación  la circunferencia con centro.

La circunferencia con centro fuera del origen con centro en el origen se determina por la ecuación.

La ecuación general se calcula desarrollando los binomios al cuadrado e igualando la ecuación a 0, obteniendo una ecuación de la forma:

Para resolver un problema de aplicación se debe diseñar el boceto donde se expresan los elementos de la circunferencia identificando las variables e incógnitas que intervienen en ella

PARÁBOLA 

Para calcular los elementos de una parábola con vértice en el origen debemos identificar el valor de la distancia focal "P" los elementos importantes de una parábola son:

a) Vértice
b) Foco
c) Directriz

Las ecuaciones para calcular los elementos de una parábola con vértice en el origen son:

PARÁBOLA CON VÉRTICE FUERA DEL ORIGEN 

Ejemplo:

Pasos:
-En la formula se sustituyen los valores.
- Se despeja p.
-Posteriormente queda P es igual a 4/8.
- El resultado es 2.
-P se refiere a que es tu foco.

GEOMETRÍA DESCRIPTIVA

La geometría descriptiva se define como la rama de las matemáticas que analiza los cuerpos en el espacio representando los objetos de tres dimensiones con representaciones bidimensionales.

 Un objeto puede representarse mediante un isométrico donde se combinan todas las perspectivas o colocando cada una de las vistas mediante proyecciones (FRONTALES, LATERALES, SUPERIORES).

Para representar un punto en forma bidimencional en un plano se realiza una rotación de los planos en sentido horario de tal manera que los planos se empalmen en forma vertical, como muestra el siguiente diagrama.

La distancia horizontal recibe el nombre de ALEJAMIENTO y la vertical de COTA.

  

CONCEPTOS DE  PROYECCIÓN 

O. Identificar el concepto de proyección.

Una proyección es la representación de un objeto tridimensional en una representación bidimensional.

 Los elementos de una proyección son:

1) OBSERVADOR: Se conoce como centro de proyección y es el punto donde concurren los rayos de proyección y puede estar ubicado en cualquier parte del espacio, si tiene una distancia finita se conoce como centro de proyección propio, si se tiene una distancia infinita (los rayos de proyección son paralelos) se le denomina como proyección impropia.

2)PLANO DE PROYECCIÓN:Es un plano colocado a una distancia arbitraria donde se representa la proyección del objeto.

3)OBJETO: Es el elemento a representar.

4) RAYOS PROYECTANTES:  Son las rectas que unen el centro de proyección con los puntos del objeto y se proyectan en el plano. 

5) PROYECCIÓN: Es la representación en el plano del objeto en forma bidimensional.

TIPOS DE PROYECCIÓN.

De acuerdo a la posición del observador se pueden clasificar las proyecciones como se representa en el siguiente esquema.

A) PROYECCIÓN CÓNICA ORTOGONAL: es aquella proyección donde las líneas de proyección concurren en un punto central y estos se presentan en forma horizontal.

B) PROYECCIÓN CÓNICA OBLICUA: es aquella proyección en donde el observador y el plano de proyección se encuentra a diferente altura como muestra el siguiente esquema.

C)PROYECCIÓN PARALELA ORTOGONAL: es aquella en donde el observador se encuentra a una distancia indefinida del plano de proyección, por tanto las líneas de proyección son paralelas.

D) PROYECCIÓN PARALELA OBLICUA: en esta proyección, las líneas de proyección se representan en forma diagonal como muestra el siguiente esquema.

Una proyección permite representar un isométrico (representación de un objeto sin alterar sus proporciones) utilizando diferentes transformaciones entre los cuales se encuentran:

A)TRASLACIÓN: es el cambio de ubicación de los puntos de una figura plana en una misma dirección, sentido y longitud, s puede representar el movimiento mediante flechas que recibe el nombre de vectores.

B)REFLEXIÓN: es una representación de una figura original a otra llamada eje de simetría utilizando rectas perpendiculares como muestra el siguiente esquema.

C) SIMETRÍA CENTRAL: en esta transformación se realiza la imagen utilizando proyecciones de los puntos de la figura que convergen en u punto llamado punto de simetría trasladando las distancias con el compás. 

 D) ROTACIÓN: esta transformación se realiza a partir de un punto de rotación determinado, se realiza en forma positiva en sentido anti-horario y en negativa en sentido horario.

Ejercicio:

Realice un triángulo de 3,6,6 y realice la traslación a 9 cm.

Pasos:

1.- Marque la base de 3 cm.

2.- Abra el compás a 6 cm.

3.-Coloque el compás en el puno A, y trace una linea.

4.- Coloque el compás en el puno B, y trace una línea.

5.- Forme el triángulo.

6.- Con la regla trace una linea desde el punto A de 9 cm.

7.-Con la regla trace una linea desde el punto B de 9 cm.

8.-Con la regla trace una linea desde el punto C de 9 cm.

9.- Finalmente trace su triangulo que se forma con las lineas anteriores.

ISOMÉTRICO.

O. Representar un objeto en un sistema tridimensional.

Un isométrico representa un objeto en forma tridimensional utilizando proyecciones con una inclinación de 30° con respecto a la horizontal para conservar las medidas ya sea a escala o con su valor real.

Ejercicio:

Realice un cubo de 4 cm de aristas en un simétrico.

1.- Marque una linea de 8 cm, posteriormente marque una linea de 6 cm sobre la misma.

2.- Con el transportador marque de lado derecho e izquierdo un angulo de 30°, marque las lineas.

3.- Marque la base de 4 cm de lado derecho.

4.- Marque la profundidad de lado izquierdo de 4 cm.

5.- Marque la altura de 4 cm en el centro. 

6.-Colo que las escuadra de 45° y de 30° de manera que la escuadra de 30° quede alineada con la linea marcada del lado izquierdo para trazar las aristas,

ISOMETRICAS.

O.representar un objeto en isometricas.

La escala se define como una representación de un objeto en forma proporcional donde  se puede calcular la proporción mediante la siguiente ecuación:

ESCALA=DIBUJO/REALIDAD

Cuando se realiza una representación donde se incremente los valores de cada magnitud la relación debe ser mayor a 1, en caso contrario la relación es menor a 1.

Para representar una escala es lugar de diagonal se representa con 2:  como muestra la siguiente proporción.

2:1  5:1  100:25 AMPLIACIÓN

1:2     3:1   100:125 REDUCCION

Ejercicio:

Realice el isométrico de un prisma utilizando la escala 2:1.

1.-Trace una linea de  8 cm.un centímetro menos de la linea trace otra vertical.

2.- Marque los ángulos de 30°.

3.-Marque la base  de  6 cm.

4.-Marque la profundidad  de  6 cm.

5.-Marque la altura de  4 cm.

6.- Para trazar las demás aristas coloque las escuadra de manera que queden ala misma posición que la linea de profundidad.

SISTEMA DE COORDENADAS.

O. Representar un punto en el espacio, calculas la medidas de las aristas de un objeto.

Un sistema de 3 dimensiones cuentas con 3 ejes  perpendiculares entre sí, los cuales permiten ubicar un punto en el espacio mediante proyecciones en cada uno de los ejes los cuales forman octantes que son proyecciones en planos formados por los ejes.

Los octantes  se colocan en sentido anti.horario indicando en la vista frontal del observador.

Para ubicar un punto en el espacio se utiliza por convención los ejes X,Y,Z  en la siguiente posición

Para representar un punto se hacen proyecciones como se indica:

a= pto. (3,4,2)

b= pto. (3,0,1)

c= pto (-2,4,0)

Para calcular la distancia entre dos puntos se utiliza teorema de pitágoras  utilizando el incremento en cada uno de los ejes.

.

PUNTO DE ESPACIO TRIDIMENSIONAL.

O. Identificar las coordenadas y las aristas de un objeto.

para identificar las vértices y aristas de un objeto es importante identificar el punto de referencia sonde será colocado el sistema de coordenadas de cada una de las vertices.

Las coordenadas permiten encontrar las mendidas de dos aristas considerando la distancia entre los puntos.

 Pasos para resolver:

1.- trazas los ejes x,y,z.

2.-Tazas tu figura de acuerdo al eje donde se ubique.

3.- A cada arista colocales una letra del abecedario para que sea mas fácil identificarlos.

4.- Toma de referencia los cuadritos para ubicar la posición de la arista.

5.- Por ejemplo si ubicamos la arista A sus coordenadas serían (0,0,0) porque no se mueve para ninguno delos ejes X y Z.

VISTAS DE UN OBJETO.

O. Identificar la proyección de las caras de un objeto.

Un objeto (Prisma) cuenta principalmente con 6 caras que pueden representarse mediante proyecciones  como muestra el siguiente esquema.

Ejercicio:

Pasos:

1.- Realiza tu prisma.

2.- Traza todas las lineas imaginarias de 30° tomando como referencia todas las aristas de tu prisma.

3.- Una vez trazado las lineas imaginarias, abre tu combas a 5 cm.

4.- Colocado el cada una de las aristas y marca con una pequeña linea.

5.- Repite los mismos pasos en cada cara de tu prima.

  ÁNGULOS.

O. Identificar la magnitud de un angulo con ecuaciones.

Un angulo se define como la abertura entre dos rectas , seguido d elos puntos que conforman al segmento a su vértice.

En el sistema internacional se utiliza los degradientes que dividen a una circunferencia en 360°.

El sistema absoluto utiliza radianes que son la división de una circunferencia de 2π radianes.

Para calcular el valor de 1 o varios ángulos a partir de un esquema se debe encontrar la ecuación como muestra el siguiente ejemplo:

PASOS:

1.-Formula la ecuación empezando por la letra A.

2.- Una vez realizado la ecuación, se suman toas las x, después se hace la operación de los números sin x.

3.- Una vez obtenido el resultado de la ecuación se multiplica cada numero por el resultado de la ecuación anterior.

4..- al terminar las multiplicaciones se sumara los resultados que se obtuvieron, y al final de la suma ese será tu resultado.